Ondas

Una onda se puede definir, en términos simples, como una perturbación que se propaga a lo largo de una dirección dada con una cierta velocidad y que implica un transporte de energía sin transporte de materia.

Las ondas pueden ser mecánicas o electromagnéticas. Las ondas mecánicas requieren de un medio, como por ejemplo el aire o el agua, para propagarse, y utilizan las propiedades elásticas del medio para hacerlo. Al someter un punto de un medio continuo a una perturbación de pequeña magnitud, las fuerzas elásticas actúan produciendo oscilaciones que se transmiten a los puntos vecinos permitiendo de esta forma que la onda se propague. Las perturbaciones se suponen de pequeña amplitud, pues de lo contrario originarían una deformación permanente en el medio.

Las ondas mecánicas pueden clasificarse en general en :

(I) Ondas transversales: Son aquellas en las que la deformación tiene lugar en la dirección perpendicular a la dirección de propagación de la onda, como por ej. una onda que se propaga en una cuerda tensa.

(II) Ondas longitudinales: Son aquellas en las que la deformación tiene lugar en la misma dirección que la de propagación de la onda, como por ej. las ondas en un resorte o una onda de presión en el aire (sonido).

Las ondas mecánicas pueden también ser combinaciones de ambos tipos de ondas, como ocurre con las ondas superficiales en un lago o con las ondas sísmicas.

Las ondas electromagnéticas, por el contrario, no requieren de un medio para propagarse: Pueden propagarse en el vacío. Estas ondas incluyen las ondas de radio, las microondas, la radiación infrarroja, la luz, la radiación ultravioleta, los rayos X, los rayos gamma, etc., las cuales difieren entre si en la frecuencia de la onda. Son ondas transversales, que se propagan todas a la velocidad de la luz c.

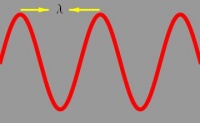
Longitud de onda

La longitud de onda identificada con la letra griega λ es la distancia entre dos puntos idénticos de una onda, como por ej. la distancia entre dos picos o crestas. La figura muestra una onda viajera, que representa, por ej. una perturbación que se propaga a lo largo de una cuerda tensa. En ella se señala la longitud de onda.

.

La longitud de onda se mide en metros. Por ejemplo en el caso de una onda de luz, que es una onda electromagnética (estas ondas son transversales) la longitud de onda más corta del espectro visible, llamamos así a la fracción del espectro electromagnético para la cual nuestra vista es sensible) corresponde aproximadamente a la longitud de onda de 400 nanometros (es decir al color violeta) y el otro extremo, a la longitud de onda más larga que es de 800 nanometros, y corresponde al color rojo. Un nanometro es la mil millonésima parte de 1 metro.

Frecuencia de una onda

Representa el número de crestas ó máximos por segundo que vemos en un punto fijo de la cuerda. Cuando damos un impulso a la cuerda en algún punto, esta perturbación se propaga a lo largo de la misma. Si nos fijamos en un punto de la cuerda al ser alcanzado por la perturbación éste comienza a oscilar. A medida que transcurre el tiempo cada punto oscila entre una amplitud máxima, digamos A y una mínima (-A). la frecuencia de la oscilación es el número de máximos o crestas en ese punto por unidad de tiempo. Si durante un segundo contamos 5 crestas, diremos que la frecuencia, que se mide en Hertz o inversa de segundo, es de 5 Hz. por ende la onda tendrá una frecuencia de 5 Hz. La longitud de onda y la frecuencia están relacionadas ya que λ x f= v, donde v representa la velocidad de propagación de la onda en el medio. Si se trata de una onda electromagnética viajando en el vacío esta velocidad es c, es decir la velocidad de la luz.

Propagación de la onda

.

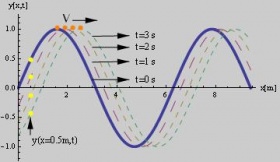
En la figura se observan distintas instantáneas (formas de la onda para diferentes instantes de tiempo) de una onda viajera transversal que se propaga hacia la derecha con velocidad v. Este tipo de onda como se mencionó se puede generar en una cuerda tensa. La función matemática que describe la onda depende del tiempo t, (medido en segundos), y de la posición x (por ej. medida en metros). Para representarla fijamos ó bien el tiempo, ó la posición. Si fijamos el tiempo (tomamos una foto) podemos ver la forma de la onda en función de la distancia. En la figura se puede ver la evolución, para los distintos tiempos, del máximo indicado por la secuencia de los 4 puntos anaranjados horizontales. O si queremos ver el movimiento de un punto particular, nos paramos en un punto fijo de la cuerda oscilante, por ejemplo veánse los 4 puntos amarillos verticales que representan como se mueve el punto de la cuerda y(x=0,5m, t), es decir, el punto de la cuerda a una distancia de 0,5m del origen para distintos tiempos: t=0 seg, es decir el instante donde comenzó a registrarse el movimiento, 1 seg, 2 seg., etc., así vemos como evoluciona este punto en función del tiempo.

Superposición de ondas: Interferencia

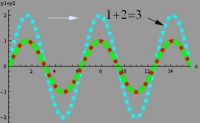
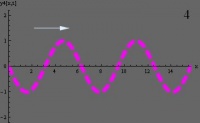
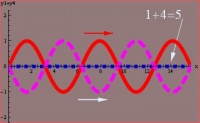
La superposición de dos o más ondas da lugar al fenómeno de interferencia. Este fenómeno puede producir, dependiendo de la relación entre la amplitud y las fases de las ondas que se superponen, una intensificación o una atenuación de la perturbación. En el primer caso se habla de interferencia constructiva, ya que las ondas al combinarse refuerzan su efecto. Cuando las ondas están en fase el efecto es máximo, y se dice que la interferencia es perfectamente constructiva. Vemos en las figuras 1, 2 y 3 ejemplos de este efecto.

En las figuras 1 y 2 vemos dos ondas viajeras. Estas ondas viajan a lo largo de una cuerda tensa y ambas poseen idéntica amplitud y fase, si ambas se hacen pasar en forma simultánea por la cuerda, se superponen sus efectos (las ondas se suman) y se genera una onda resultante cuya amplitud es el doble de la de cada una de ellas, y que tiene la misma fase que las anteriores, como se ve en la figura 3. Este fenómeno se denomina interferencia completamente constructiva.

Si las ondas no están en fase al superponerlas se atenúa el efecto, siendo esta atenuación, también de diferentes grados. Si las ondas tienen fase opuestas pero diferente amplitud la atenuación no llega a ser completa. La atenuación completa se produce cuando, además de tener fases opuestas, las ondas que se superponen poseen igual amplitud, dando lugar a una interferencia destructiva completa.

En la figuras ambas ondas 1 y 4 viajan en el mismo sentido, poseen la misma amplitud, pero sus fases son opuestas. Al superponerse el efecto final dará una perturbación nula ( figura 5). La cuerda no muestra ninguna oscilación. Este fenómeno se denomina interferencia completamente destructiva.