Centenario de Difracción de Rayos-X. Los Bragg

(Parte II. Por Oscar Piro.)

En 1912 William Henry Bragg, físico Británico. (Fig. izq.) era Profesor de Física en la Universidad de Leeds, Inglaterra, donde se traslada en 1908 desde la Universidad de Adelaida, Australia. En Leeds extiende su estudio previo sobre la ionización de los gases por rayos-α a los rayos-X, utilizando en este último caso la radiación característica del ánodo de tubos de vacío. Era un ferviente creyente en una interpretación corpuscular de los rayos-X (por entonces, creencia muy popular en Inglaterra), debido a la observación de fotoionización atómica excitada por estos rayos. El hijo de Bragg, William Lawrence Bragg, físico Británico (Fig. derecha), seguía los pasos profesionales de su padre estudiando Física como tema principal. Después de una formación inicial en Física y Matemáticas en la Universidad de Adelaida, completa su formación en Física en el Laboratorio Cavendish de la Universidad de Cambridge, Inglaterra, bajo la dirección de J. J. Thomson, obteniendo su primer nombramiento como Profesor en el Trinity College en 1911.

No está claro cómo las noticias del descubrimiento de Laue llegaron a Inglaterra y, particularmente, a W. H. Bragg. Pudo haber sido a través copias de las publicaciones enviadas por el mismo Laue o a través de científicos Alemanes que asistieron en Julio de 1912 al 250º aniversario de la Royal Society celebrado en Londres. Información completa y detallada sobre el trabajo parece, sin embargo, haber llegado a Bragg a través de una conferencia dictada por Thomson ante el grupo de Física en Leeds (o Manchester) un poco más tarde. Por entonces se encontraban disponibles reproducciones de los diagramas de Laue y W. H. Bragg se las hace conocer a su hijo para emprender juntos un estudio independiente del nuevo fenómeno durante el verano de 1912 en Leeds. Inicialmente trataron la posibilidad de explicar los patrones de Laue por alguna otra hipótesis diferente de la difracción de ondas. De hecho, W. L. Bragg hizo algunos experimentos infructuosos para ver si había alguna evidencia de 'corpúsculos de rayos- X' mediante la irradiación a lo largo de ‘avenidas’ formadas entre hileras de átomos en un cristal. (1)

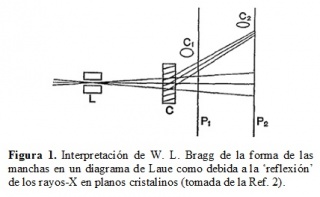
Al ver que los esfuerzos para explicar los resultados de Laue en el marco de una teoría corpuscular no conducían a ninguna parte, W. L. Bragg comenta en un relato de 1943: "De regreso a Cambridge para reflexionar sobre el trabajo de Laue, sin embargo, me convencí de la exactitud de su deducción que el efecto era uno de difracción de ondas, pero también me convencí que su análisis sobre la forma en que se lleva a cabo no era correcta". Una pista sobre la correcta interpretación del fenómeno fue sugerida por la siguiente observación de W. L. Bragg sobre la forma de las manchas de difracción en la placa radiográfica (ver Fig. 11). "Cuando la placa se coloca en P1 cerca del cristal las manchas eran casi circulares como C1, pero cuando se la coloca más lejos en P2 se volvieron muy elíptica (C2). Laue había atribuido su patrón a la difracción de ciertas longitudes de onda específicas en el haz de rayos-X por el arreglo regular del cristal. Dada una longitud de onda fija, la teoría óptica nos dice que la difracción debe llevarse a cabo en un ángulo definido, y esto significa que los rayos difractados dibujados en la figura deberían ser todos paralelos. Había oído a J. J. Thomson hablar durante una conferencia sobre la teoría de Stokes de los rayos-X como pulsos muy cortos de radiación electromagnética. Descubrí que esos pulsos sin una longitud de onda definida deben ser difractados no sólo en ciertas direcciones, sino que deben ser eyectados en cualquier ángulo de incidencia por los planos de átomos en el cristal, como si estos planos fueran espejos. Un vistazo a la geometría de la figura en que los rayos se dibujan como si fueran reflejados, muestra que ellos se acercan entre sí verticalmente mientras continúan extendiéndose horizontalmente, de esta manera explicando por qué las manchas se vuelven más elípticas a medida que la placa se coloca más lejos"

Esta observación conduce a Bragg a interpretar el patrón de difracción de rayos-X como debido a la interferencia entre los rayos reflejados por los átomos ubicados en familias de planos cristalinos paralelos. Estos planos se comportarían ante los rayos-X de manera similar a como lo hace en Óptica un arreglo paralelo de espejos igualmente espaciados y semitransparente ante luz incidente. Por lo tanto, la condición de interferencia constructiva para los rayos-X reflejados vendría dada por:

[math]\displaystyle{ 2d \cos\theta = n \lambda \,\lt math\gt : Ecuación de Bragg, donde : * d = separación entre planos adyacentes en la familia *\lt math\gt \theta \lt math\gt = ángulo del haz incidente con la normal al plano *\lt math\gt \lambda\lt math\gt = longitud de onda de los rayos-X * n = orden de difracción "Quedaba por explicar por qué algunos de estos espejos atómicos en el cristal de blenda de zinc reflejaban más intensamente que otros, una dificultad que había conducido a Laue a postular un grupo de longitudes de onda definidas. William J. Pope y William Barlow sostenían la teoría que los átomos en compuestos cúbicos como ZnS se empaquetan juntos, no como bolas en los vértices de una pila de cubos, sino en lo que se llama ‘empaquetamiento cúbico compacto’, donde las bolas se disponen también en el centro de las caras del cubo (ccc). Intenté ver si esto podría explicar la anomalía, ¡y así lo hizo! Estaba claro que el arreglo de los átomos en blenda de zinc era del tipo centrado en las caras. Tuve cuidado de llamar mi artículo sobre la estructura de la blenda de zinc ‘The Diffraction of Short Electromagnetic Waves by a Crystal’ ('La Difracción de Ondas Electromagnéticas Cortas por un Cristal') (2) porque todavía no estaba dispuesto a renunciar al punto de vista de mi padre que los rayos-X fueran partículas; pensé que posiblemente podrían ser partículas acompañadas por ondas". A pesar que en este primer trabajo W. L. Bragg determinó la correcta red de Bravais de ZnS (ccc), sin embargo el mismo no describe la estructura detallada del compuesto. '''Las Primeras Determinaciones de Estructuras Cristalinas''' W. J. Pope, quien era Profesor de Química en Cambridge, sugirió a W. L. Bragg el aplicar su método estructural de rayos-X a los cristales de haluros alcalinos, a saber: NaCl, KCl, KBr y KI. Resultó que los diagramas de Laue originados por dichas sales eran más simples que los de blenda de zinc, permitiendo una solución completa de sus estructuras. Estos fueron los primeros cristales analizados por difracción de rayos-X. (3) Revisaremos aquí el enfoque cualitativo de Bragg para determinar la estructura cristalina de la serie isomórfica de haluros alcalinos, basado en consideraciones de simetría de la red cristalina, la magnitud de dispersión atómica (que provisionalmente atribuyó al peso atómico A en lugar del correcto número atómico Z), la 'reflectividad' relativa de planos cristalinos basada cualitativamente en la distribución de los átomos que yacen sobre dichos planos, [[Imagen:Fig2BCRX.jpg|400px|right|]] y empleando sistemáticamente su ecuación y una buena dosis de conocimientos de Física y Química. De esta manera demuestra que los datos de difracción sustentan el modelo propuesto consistente en dos redes cúbicas ccc intercaladas, una constituida por iones alcalinos, la otra por iones haluros, y desplazadas relativamente entre sí a lo largo de un eje de celda en la mitad de su tamaño. En la figura 2: Estructura tipo sal de roca de haluros alcalinos. Los discos negros indican los iones alcalinos (haluros) y los abiertos los contra-iones haluros (alcalinos). AB = a: constante de celda cúbica. Bragg considera reflexiones en tres planos principales, esto es (200), (220), que llamó inconvenientemente planos (100) y (110), y (111). Para una red de Bravais cúbica simple (cs), las distancias entre planos vecinos en cada familia están en la relación: \lt math\gt 1:\frac{1/\sqrt{2}:1/\sqrt{3} }[/math]

pero por aquélla época no se disponía de datos de rayos-X para dicha red. Sin embargo, Bragg notó que esta red cs (con una constante de celda igual a la mitad de la celda de la Fig. 2) podría ser simulada por el cloruro de potasio (silvina) en razón que los rayos-X incidentes interactuarían con dispersores casi idénticos, dado que potasio y cloro se encuentran próximos entre sí en la Tabla Periódica. De hecho, no observó intensidad difractada para la reflexión (111). Entonces Bragg mide las intensidades de reflexiones en la familia de planos (200) conteniendo NaCl, es decir AABT, dbfh, etc. de la Fig. 2, la familia (220) también conteniendo NaCl, a saber BDHF, adhe, etc y la familia (111) consistente en planos de Na y Cl intercalados, tales como BDE (Na), adl (Cl), etc. Las distancias repetitivas entre planos de estas familias están en las proporciones

[math]\displaystyle{ 1:\frac{1/\sqrt{2}:1/\sqrt{3} }[/math]

De esta manera, Bragg contaba con datos experimentales de difracción de rayos-X que le permitieron validar la propuesta de una red de Bravais cúbica ccc para la serie de haluros alcalinos. De hecho, interpretó la intensidad nula observada para la reflexión (111) en KCl como debida a los efectos de cancelación casi perfectos entre la reflexión de rayos-X en los planos adyacentes BDA (K) y adl (Cl) de la red (ver Fig. 2). Además, consideraciones similares lo llevaron a interpretar la débil intensidad observada para la línea (111) en NaCl como también debida a interferencia entre reflexiones en los planos anteriores que, a pesar de estar en oposición de fase, poseen diferentes amplitudes debido a la diferencia de poder de dispersión de los iones de Na y Cl, dando lugar a una interferencia parcialmente destructiva de las ondas reflejadas. Con argumentos similares, Bragg pudo igualmente interpretar el patrón de difracción de KBr y KI como debido principalmente a una sola red cúbica ccc de iones haluros, dado que estos poseen un poder de dispersión atómica a los rayos-X mucho mayor que su contraparte alcalina.

El Espectrómetro de Rayos-X

Con el fin de examinar el rayo reflejado con más detalle, W. H. Bragg construye un espectrómetro de rayos-X. En este instrumento, la cara de un cristal puede orientarse de manera que refleje los rayos-X en cualquier ángulo y la intensidad de la radiación correspondiente medirse con precisión mediante una cámara de ionización. Con este instrumento, W. H. Bragg realiza un gran descubrimiento. Además de la radiación de rayos-X continua (bremsstralung) conteniendo un intervalo de longitudes de onda (que W. L. 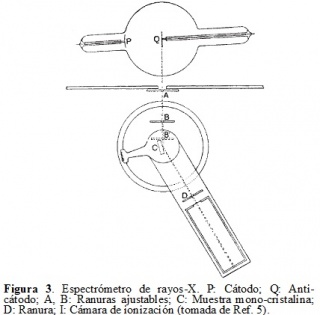Bragg había llamado ‘pulsos de rayos-X’), encuentra que cada metal usado como fuente de radiación (anticátodo) en el tubo de rayos-X producía un espectro de rayos-X característico con longitudes de onda bien definidas, justamente como los elementos atómicos producen espectros en la región óptica.(5) Con este hallazgo W. L. Bragg establece los fundamentos del área de la Física conocida como Espectroscopia de Rayos-X. El espectrómetro de rayos-X (ver Fig. 3) resulta ser un método para analizar estructuras cristalinas más poderoso que el método fotográfico de Laue y colaboradores, usado inicialmente por W. L. Bragg.

Con este instrumento se puede examinar en sucesión los distintos planos cristalinos y, midiendo los ángulos y la intensidad con que se reflejan los rayos-X en dichos planos, se podría deducir la manera en que se encuentran arreglados los átomos en una red. Por otro lado, una cara cristalina adecuada podría utilizarse para determinar la longitud de onda de los rayos-X característicos de diferentes elementos empleados como fuentes. De esta manera puede seleccionarse un haz monocromático de rayos-X mediante reflexión en un cristal (monocromador). W. H. Bragg mide las longitudes de onda de los espectros de rayos-X característicos producidos por los elementos platino, osmio, iridio, paladio, rodio, cobre y níquel y los identifica con las radiaciones K y L descubiertas por Barkla. Calcula la energía cuántica de los fotones de rayos-X mediante la relación de Planck, demostrando que acuerda con la energía de los rayos catódicos necesaria para excitarlos. Muestra que las longitudes de onda más cortos (líneas Kα y Kβ) de diversos elementos eran similares y aproximadamente inversamente proporcionales al cuadrado del peso atómico. Esto era en realidad un primer indicio de la posterior generalización de este principio establecida por Henry G. J. Mosely, quien lo utilizó para determinar el número atómico de los elementos. También midió los bordes de la absorción, esto es las longitudes de onda críticas para las cuales se observa un abrupto cambio en la absorción de rayos-X por parte de los elementos. (6)

Mediante el uso de las mediciones en mono-cristales con el espectrómetro de rayos-X, muchas de ellas debidas a Bragg padre, W. L. Bragg pudo resolver las estructuras de blenda de zinc, fluorita, cuprita, pirita de hierro, nitrato de sodio y del grupo calcita de minerales (7). Zinc y fluorita resultaron los más simples porque (como en el caso de los haluros alcalinos) los átomos ocupan posiciones especiales en el cristal; pirita y calcita son más difíciles dado que la localización del azufre y del ion carbonato no está fija por simetría en sus respectivos cristales y por lo tanto, encontrar sus posiciones requieren un estudio más complicado (involucrando uno o más parámetros estructurales ajustables) que los llevado a cabo por los Bragg hasta entonces

W. H. y W. L. Bragg fueron galardonados conjuntamente en 1915 con el Premio Nobel de Física "por sus servicios en el análisis de la estructura cristalina por medio de rayos-X"

Epílogo.

Para cristales con alta simetría de compuestos simples, donde los átomos yacen en puntos de red, los ‘planos de átomos reflectantes’ imaginados por Bragg resultó una noción útil para resolver las primeras estructuras. Sin embargo, aún para cristales un poco más complejos, el concepto de ‘planos reflectantes’ carece de sentido dado que en general los átomos no se encuentran arreglados según tales planos cristalinos, los que realmente constituyen objetos matemáticos en lugar de físicos. El concepto de ‘planos reflectantes’ fue pronto reemplazado por el de capas de reflectividad modulada, las que fueron representadas por series de Fourier, un avance anticipado por W. H. Bragg (8) y luego elaborado por otros. Muy pronto resultó también claro que los ligeros electrones atómicos eran los que dispersaban apreciablemente los rayos-X; en efecto, los núcleos atómicos son demasiado masivos para seguir las rápidas oscilaciones de esta radiación EM (de alrededor de un trillón de ciclos por segundo). Para progresar en la determinación de estructuras cristalinas mas allá de los métodos semi- cuantitativos desarrollados principalmente por los Bragg durante la primera mitad de la década de 1910, se requería:

1) Una mejor descripción de los fundamentos físicos subyacentes en el fenómeno de difracción de rayos-X por átomos, moléculas y sólidos.

2) Una descripción matemática detallada del poder dispersivo de cristales (series de Fourier).

3) Desarrollo de métodos generales ab initio (Patterson, métodos directos, métodos basados en la dispersión atómica anómala, etc.) para resolver el llamado ‘problema de las fases’ en Cristalografía.

4) Mejoramiento e incremento en la potencia de las fuentes de rayos-X (tubos de vacío de rayos-X de Coolidge, radiación-X por ánodos rotatorios, radiación sincrotrónica, láseres de rayos-X).

5) Incremento sustancial en la capacidad de cálculo (desarrollo de computadores electrónicos)

En una futura contribución al presente ensayo, nos apartaremos del desarrollo histórico relatado aquí para describir los avances en la solución de los requerimientos anteriores producidos durante los últimos 100 años y que constituyen la moderna Cristalografía Estructural.

Bibliografía:

1. W. H. Bragg, “X-ray and crystals”, Nature (London) 90, pp. 219 (1912).

2. W. L. Bragg, “The Diffraction of Short Electromagnetic Waves by a Crystal”, presentado a la Proceeding of the Cambridge Philosophical Society en Noviembre 1912 y publicado luego en Proc. Cambr. Phil. Soc. 11, pp. 43-57 (1913).

3. W. L. Bragg, “The Structure of Some Crystals as Indicated by Their Diffraction of X-rays”, Proc. Roy. Soc. A89, pp. 248-277 (1913).

4. W. L. Bragg, “The Specular Reflection of X-rays”, Nature 90, Issue 2250, pp. 410 (1912).

5. W. H. Bragg, “The X-ray spectrometer”, Nature 94, Issue 2347, pp.199-200 (1914).

6. W. H. Bragg, “Bakerian Lecture: X-Rays and Crystal Structure”, Phil. Trans. R. Soc. Lond. A215, pp. 253-274 (1915).

7. W. L. Bragg, “The Analysis of Crystals by the X-ray Spectrometer”, Proc. R. Soc. A89, pp. 468-489 (1914).

8. W. H. Bragg, “Bakerian Lecture: X-Rays and Crystal Structure”, Phil. Trans. R. Soc. Lond. A215, 253-274 (1915).