100 años de la teoría de la relatividad general
En Noviembre de 1915 A. Einstein publica las ecuaciones definitivas de su Teoría General de la Relatividad, uno de los pilares (junto con la mecánica cuántica) de la física moderna y base de la cosmología. Con este trabajo Einstein presentaba una forma no sólo más precisa sino también conceptualmente muy diferente de entender la gravedad. Pero como su nombre lo sugiere, estos artículos son la culminación del trabajo empezado en 1905 con la publicación de su Teoría Especial de la Relatividad[1].
Una idea feliz: El principio de equivalencia
En 1905 Einstein publicaba "Sobre la electrodinámica de cuerpos en movimiento", el primer artículo sobre relatividad, en el que mostraba cómo el reconsiderar las ideas establecidas por Newton sobre el espacio y el tiempo derivaba en una solución natural a ciertas paradojas que impedían reconciliar la teoría electromagnética con la mecánica [2]. Su teoría de la relatividad resolvía las inconsistencias asociadas al electromagnetismo, pero resultaba inconsistente con otra teoría exitosa: La teoría newtoniana de la gravedad. La ley de gravitación universal de Newton descansa sobre los supuestos newtonianos sobre el espacio y el tiempo, por lo que con la llegada de la relatividad especial se hizo necesario encontrar una nueva teoría de la gravedad, acorde a la nueva noción de espacio-tiempo. El nacimiento de la teoría general de la relatividad podría situarse en 1907. Einstein trabajaba (todavía) en la Oficina de Patentes de Berna cuando tuvo una ocurrencia, que más tarde él mismo llamaría "la idea más feliz de mi vida": "Estaba sentado en la oficina de patentes de Berna, en 1907, cuando, de repente, me vino una idea: una persona en caída libre no sentirá su propio peso. Quedé sorprendido. Esa sencilla idea me causó una profunda impresión y me impulsó hacia una teoría de la gravitación"
De esta revelación nació lo que hoy conocemos como el principio de equivalencia. Imaginemos por un momento que estamos dentro de una cabina que nos aísla completamente del exterior. Si tomamos una pelota a cierta altura respecto del piso y la soltamos, observamos que cae tal y como estamos acostumbrados a observar que sucede debido a la gravedad terrestre. Podríamos pensar entonces que nuestra cabina se encuentra en reposo respecto a la superficie terrestre, pero ese no es necesariamente el caso. La cabina podría estar en algún lugar del universo, suficientemente lejos de cualquier cuerpo masivo (y por lo tanto fuera de la influencia de campos gravitatorios), pero acelerando en dirección normal a la superficie del piso de la cabina, a unos 9.81 m.s^-2. En esas condiciones, al soltar un objeto lo veríamos acelerar hacia el suelo tal y como lo haría debido a la influencia del campo gravitatorio terrestre. De manera que desde nuestro sistema de referencia, solidario a la cabina, no podemos distinguir las siguientes situaciones: a) La pelota cae hacia la Tierra, b) El piso de la cabina acelera en dirección a la pelota. Por el contrario, supongamos que flotamos (y con nosotros cualquier otro objeto) dentro de la cabina, como si no tuviéramos peso. ¿Puede inferirse de este hecho que la cabina se encuentra fuera de la influencia de todo campo gravitatorio? No realmente. La cabina podría encontrarse en caída libre dentro de un campo gravitatorio, en cuyo caso observaríamos exactamente lo mismo. De nuevo, desde dentro de la cabina es imposible distinguir entre estas dos situaciones. Einstein se convenció entonces de que esta imposibilidad de distinguir un sistema de referencia acelerado de uno inmerso en un campo gravitacional no debía restringirse a cuerpos en caída, sino que debía ser válido para cualquier medición que uno quisiera hacer: No existe experimento que permita distinguir un referencial en caída libre de uno inmerso en un campo gravitacional. Este es el principio de equivalencia. La consecuencia directa de este principio es que un sistema de referencia en caída libre no puede distinguirse de un sistema de referencia en un espacio libre de gravedad. En otras palabras: En un sistema de referencia en caída libre las leyes de la física son las mismas que aquellas de un universo sin gravedad, que son precisamente las leyes de la relatividad especial.
Esto último es cierto, pero no completo. Hay una suposición implícita en el argumento anterior, y es que estamos pensando en un campo gravitatorio homogéneo, es decir, suponemos que hay una dirección (hacia abajo) en la que caen los objetos. Esto es cierto en buena aproximación, por ejemplo, si nuestros experimentos se restringen a pequeñas áreas sobre la superficie terrestre, de manera que podamos despreciar la curvatura del planeta y definir una "vertical". Pero si nuestra hipotética cabina es suficientemente grande, los objetos no van a acelerar simplemente hacia abajo, sino que van a acelerar una hacia otra también. Esta aceleración, llamada aceleración de marea, ciertamente permitiría distinguir si nuestra cabina acelera en un espacio sin gravedad. De manera que el principio de equivalencia requiere una formulación un poco más precisa: No existe experimento que permita distinguir un referencial en caída libre de uno inmerso en un campo gravitacional, siempre que los efectos de marea sean despreciables. La condición de que los efectos de marea sean despreciables puede traducirse en una restricción de los experimentos a una región suficientemente pequeña del espacio. Podemos decir entonces que un sistema de referencia inmerso en un campo gravitatorio es localmente equivalente a un sistema acelerado en un espacio sin gravedad, y por lo tanto, localmente, las leyes de la física son aquellas de la relatividad especial.
Consecuencias directas del principio de equivalencia
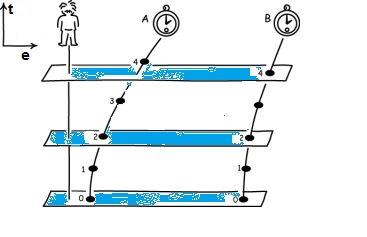
Del principio de equivalencia se deducen tres importantes consecuencias, que Einstein derivó entre 1907 y 1911: En un campo gravitatorio la luz debía "doblarse" y reducir su velocidad, y el tiempo mismo debía dilatarse. LOS RELOJES CORREN MAS LENTO Supongamos ahora que tenemos dos relojes en reposo uno respecto al otro, pero acelerando respecto a un observador inercial. Esta situación puede ilustrarse con un diagrama espacio-tiempo como el de la figura 1.
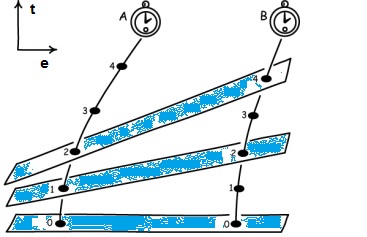
Las líneas horizontales (curvas de simultaneidad) conectan eventos simultáneos en diferentes regiones del espacio. Lo que muestran es que, para un observador inercial, el instante asignado a eventos simultáneos es el mismo en los dos relojes (por lo menos si consideramos cortos intervalos de tiempo). Si ahora nos situamos en un referencial sobre uno de los relojes (cualquiera) la situación cambia, debido a la relatividad de la simultaneidad. Un observador moviéndose con velocidad relativa uniforme respecto al primero, juzgará de manera diferente la simultaneidad entre eventos, por lo que las curvas de simultaneidad estarán inclinadas. Como los relojes aceleran, instante a instante las curvas de simultaneidad van a inclinarse más, como se muestra en la figura 2. Como las curvas conectan eventos simultáneos, los relojes asignan instantes diferentes a los mismos eventos, siendo los de B posteriores a los de A, es decir, A "atrasa" respecto a B. Si volvemos ahora al ejemplo de la cabina acelerando, el resultado es que un reloj en el techo de la cabina va a correr más rápido que uno apoyado en el piso. Pero como el principio de equivalencia nos dice que no hay cómo distinguir un referencial acelerado de uno inmerso en un campo gravitatorio, debemos concluir que los relojes dentro de un campo gravitatorio corren más y más lento cuanto más cerca estén de la fuente del campo. Este efecto se conoce como "dilatación gravitacional del tiempo". Un argumento muy similar muestra, también, que un pulso de luz se propagará más lento cuanto más "profundo" se encuentre dentro de un campo gravitacional.
Cambio en la dirección de la luz
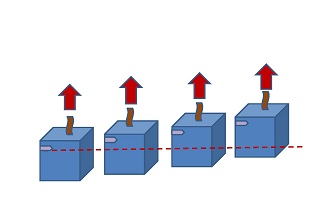
En la teoría especial de la relatividad todo observador inercial encuentra que la luz se propaga en línea recta. Volvamos a la cabina acelerando en un espacio sin gravedad, e imaginemos un pulso de luz propagándose en dirección normal a la de aceleración. Para un observador inercial la situación sería la que se ilustra en la figura 3 de abajo: El pulso se propaga en línea recta en dirección horizontal, al tiempo que el piso de la cabina acelera hacia el mismo.
Para un observador dentro de la cabina, sin embargo, la situación es diferente. Este observador encontrará que la luz "cae" hacia el piso de la cabina, tal como lo haría cualquier otro objeto. De manera que en el referencial acelerado, dentro de la cabina, la trayectoria del pulso de luz no será recta sino curva, hacia el piso. El principio de equivalencia nos dice entonces que, en presencia de un campo gravitatorio, la trayectoria de la luz tiende a doblarse hacia la fuente del campo. Este efecto, predicho por Einstein mucho antes incluso de tener las ecuaciones correctas que modelan el campo gravitatorio, fue observado el 29 de mayo de 1919 durante una expedición a Sudáfrica liderada por el astrónomo inglés Arthur Eddington.
La ilusión de gravedad: Espacio tiempo curvo
Para 1912 Einstein era ya consciente de que las transformaciones de Lorentz dejarían de ser válidas en un universo con gravedad, debido a la validez local del principio de equivalencia, pero no tenía todavía las ecuaciones que describen el campo gravitatorio. Sus primeros intentos apuntaron a desarrollar una teoría de la gravedad en la que la velocidad de la luz fuese variable, pero no tuvo éxito. Finalmente, en el mismo año de 1912 dio con la idea correcta: "Si todos los sistemas de referencia acelerados son equivalentes, entonces la geometría euclídea no puede valer en todos ellos."
Lo que esto significa es que en un universo con gravedad el espacio-tiempo no puede ser plano como lo es en la teoría especial de la relatividad, sino que debe tener curvatura, la cuál debe ser determinada por la distribución de materia y energía. Lo que entendemos por "gravedad" pasa a ser "curvatura del espacio-tiempo", los referenciales en caída libre en un campo gravitatorio son entendidos como observadores que se mueven por las curvas geodésicas del espacio tiempo. En palabras del físico John Wheeler: el espacio-tiempo le dice a la materia cómo moverse, y la materia le dice al espacio-tiempo cómo debe curvarse.
Einstein se dio cuenta entonces de que su teoría de la gravedad debía ser expresada en otro lenguaje matemático, por lo que pidió ayuda a su amigo matemático Marcel Grossmann. Grossmann hizo le hizo notar que la matemática necesaria para lidiar con el problema de hallar las buscadas trasformaciones de coordenadas en un espacio-tiempo con curvatura ya había sido desarrollada 15 años atrás por los matemáticos Riemann, Ricci y Levi-Civita. Resultado de esta colaboración fue la publicación de 2 artículos, uno en junio de 1913, y otro poco más de un año después. En este último, una buena parte estaba dedicada a sentar la base matemática de una nueva teoría de la gravedad. El artículo llega a manos de Levi-Civita por medio de Max Abraham, otro físico que se encontraba también en la búsqueda de una teoría relativista de la gravedad. Levi-Civita se interesa en el trabajo de Einstein, y durante 1915 mantienen una fructífera correspondencia, que le sería de mucha ayuda a este último.
A fines de junio Einstein da una serie de conferencias en Gottinga acerca de la teoría desarrollada en colaboración con Grossmann, y gana el interés del matemático David Hilbert. Los pasos finales hacia la teoría definitiva serían dados por Einstein y Hilbert casi en simultáneo, siendo este último el primero (por unos pocos días de diferencia) en publicar las ecuaciones definitivas el 20 de noviembre de 1915.
El 25 de noviembre de 1915 culminaba el proyecto iniciado en 1905 con su primer artículo sobre relatividad, legando una teoría cuyas predicciones serían verificadas una y otra vez durante un siglo, y que es la base de la cosmología moderna[3].
Debug data: