Física y Matemática
El hermoso problema de los cuatro colores
Este es un problema matemático, pero que entusiasma mucho a los físicos, informáticos y por su puesto también a los cartógrafos y los amantes de los mapas. Es muy fácil de enunciar. Dado por ejemplo un cierto país, ¿Cuántos colores son necesarios para pintar las provincias, de modo que dos provincias que limitan entre sí (y tienen una frontera de una cierta longitud) no tengan el mismo color? El problema puede obviamente también formularse de otras maneras análogas (cuántos colores son necesarios para pintar países en un continente, o partidos en una provincia o país).
Tanto la respuesta como la historia de su demostración son realmente sorprendentes: Se necesitan solamente cuatro colores! Nunca mayor cantidad. Y esto NO es algo demostrado hace más de 2000 años, ni siquiera fue demostrado en el siglo XIX. Fue demostrado recién en 1976, ¡y por medio de computadoras!
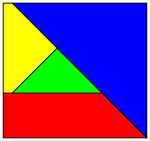
Que al menos cuatro sean necesarios es evidente de la figura derecha. Lo difícil es demostrar que solamente cuatro son necesarios. El problema implicó la introducción de nuevos conceptos tales como demostraciones asistidas por computadoras y los denominados ``Problemas polinomiales duros no deterministas´´. El tema y su generalización es en realidad aún motivo de investigación. Se han dado nuevas y mejores demostraciones en este siglo (2002 y 2005).
La respuesta correcta fue originariamente conjeturada en 1852 por Francis Guthrie, pero sin demostración.
Una de las primeras demostraciones tentativas fue realizada en 1879 por A. Kempe, pero contenía en realidad una falla, que fue descubierta 11 años después.
Lo mismo sucedió con otra prueba dada por G. Tait en 1880, que también fue probada falsa 11 años después.
Lo que sí fue correctamente demostrado en 1890 es que no se necesitaban más de 5 colores. Pero la demostración de que sólo cuatro eran suficientes fue realizada recién en 1976 por K. Appel y W. Haken. Y necesitaron la ayuda de computadoras, ya que fue necesario verificar nada menos que 1936 casos o configuraciones distintas.
Nuevas demostraciones han reducido el número de casos a verificar pero aún se requiere la ayuda de la PC!. Y en 2008 fue realizada una nueva prueba. Es un hecho notable para las matemáticas que la computadora haya sido imprescindible para su demostración. Muy recientemente el problema de los cuatro colores y las técnicas de su demostración han sido aplicadas a ciertos problemas físicos, relacionados con problemas de mecánica cuántica en materia condensada.
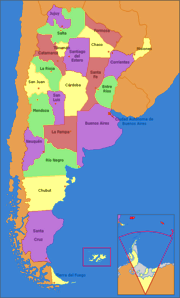
En la figura izquierda se verifica efectivamente que sólo cuatro colores son necesarios en el mapa de Argentina, a pesar de que Córdoba limita con siete provincias!
Debug data: